probabilidad-y-estadistica
Python
Estadísticas Descriptivas
Estadística descriptiva
La estadística descriptiva (descriptive statistics) es una rama de la estadística que se encarga de recolectar, analizar, interpretar y presentar datos de manera organizada y efectiva. Su principal objetivo es proporcionar resúmenes simples y comprensibles acerca de las características principales de un conjunto de datos, sin llegar a hacer inferencias o predicciones sobre una población más amplia.
Guía de la estadística descriptiva en Python
Medidas de tendencia central
Las medidas de tendencia central son valores numéricos que describen cómo se centralizan o agrupan los datos en un conjunto. Son esenciales en estadística y análisis de datos porque nos proporcionan un resumen de la información, permitiéndonos comprender rápidamente las características generales de una distribución de datos.
Para ilustrar estos conceptos, usaremos un DataFrame de Pandas.
1import pandas as pd 2import numpy as np 3 4# Creamos un DataFrame de ejemplo 5data = {'valores': [10, 20, -15, 0, 50, 10, 5, 100]} 6df = pd.DataFrame(data) 7 8print(df)
Media (mean)
Es el promedio de un conjunto de datos numéricos.
Mediana (median)
Es el valor que se encuentra en la posición central cuando los datos están ordenados.
Moda (mode)
Valor que ocurre con mayor frecuencia.
Estas medidas son fundamentales para describir y analizar distribuciones de datos.
Medidas de dispersión
Las medidas de dispersión son valores numéricos que describen cómo de variados son los datos en un conjunto. Mientras las medidas de tendencia central nos indican dónde están "centrados" los datos, las medidas de dispersión nos muestran cuánto se "extienden" o "varían" esos datos alrededor de ese centro.
Rango (range)
Es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos.
Varianza y desviación estándar (variance and standard deviation)
Ambas métricas miden cómo de lejos están, en promedio, los valores con respecto a la media. La desviación estándar es más interpretable porque está en las mismas unidades que los datos originales. Pandas calcula ambas de forma sencilla.
Medidas de forma
Las medidas de forma describen cómo se distribuyen los valores en un conjunto de datos en relación con las medidas de tendencia central. Específicamente, nos indican la naturaleza de la distribución, ya sea si es simétrica, sesgada o tiene colas pesadas, entre otros.
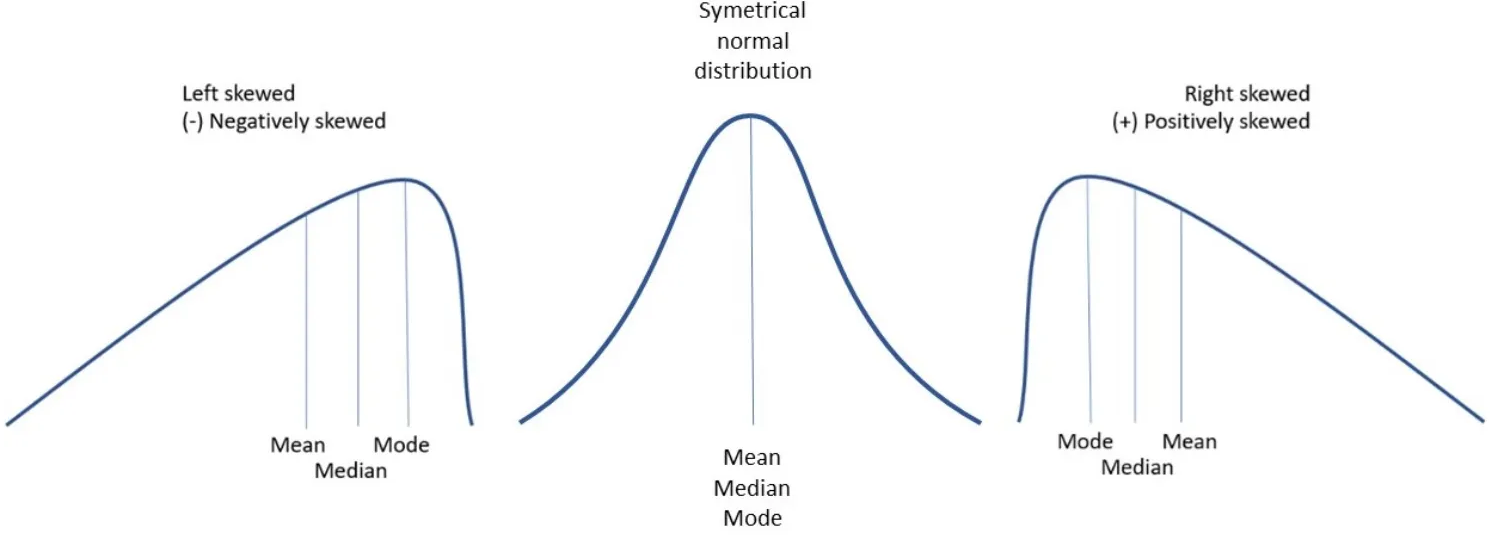
Asimetría (skewness)
Mide la falta de simetría en la distribución de datos. Una asimetría positiva indica que la mayoría de los datos están a la izquierda y hay unos pocos valores muy altos a la derecha. Una asimetría negativa indica que hay más valores bajos inusuales. Si es cercana a cero, sugiere que los datos son bastante simétricos.
Curtosis (kurtosis)
La curtosis mide la "pesadez de las colas" y la "agudeza del pico" de una distribución. En términos prácticos, nos indica la probabilidad de encontrar valores atípicos (outliers). Su utilidad es clave, por ejemplo, en el modelado de riesgos financieros, donde una alta curtosis significa un mayor riesgo de eventos extremos. Una curtosis positiva indica un pico más agudo en comparación con la distribución normal. Una curtosis negativa indica un pico más aplanado y unas colas más ligeras. Una curtosis cercana a cero es lo ideal, ya que sugiere una forma similar a la de la distribución normal.
El método df.kurt() de Pandas calcula el exceso de curtosis, lo que facilita la comparación con la distribución normal.
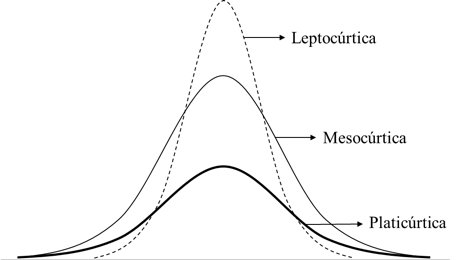
Aquí te mostramos los tres tipos principales de curtosis:
- Leptocúrtica : Distribución con un pico más agudo y colas más pesadas que la normal. Tiene más outliers. Un ejemplo es la distribución t de Student. Su curtosis de exceso es positiva (> 0), lo que en modelado financiero se traduce en mayor riesgo.
- Mesocúrtica : Distribución con una forma similar a la distribución normal. Su curtosis de exceso es cercana a cero (= 0).
- Platicúrtica : Distribución con un pico más plano y colas más ligeras que la normal. Tiene menos outliers. Un ejemplo es la distribución uniforme. Su curtosis de exceso es negativa (< 0), lo que indica un riesgo menor de eventos extremos.
Visualización de datos
Visualizar los datos es fundamental. Se suelen utilizar histogramas, gráficos de barras y diagramas de dispersión, dependiendo de la tipología de los datos.